The first of two of three blogs exploring the renin-angiotensin-aldosterone system in ME/CFS and COVID-19. Warning – this blog is complex…
Back in 1997, they had a couple of important things right – orthostatic intolerance (OI) is basically caused by not getting enough blood to the brain when one stands (or sits). Even back then, researchers knew that problem could be caused in different ways. Blood pooling in the lower body upon standing – probably because of damaged autonomic nerves – was one. Low blood volume (@75% of normal) was another factor making it difficult to get blood to the brain upon standing.
The 1997 paper, “Hypovolemia in Syncope and Orthostatic Intolerance Role of the Renin-Angiotensin System“, brought a big surprise, though. Not only did they find markedly low blood volume – in some cases 1,000 ml low (about the size of a large Coke bottle) – but they found low plasma renin activity as well – and that didn’t make sense.
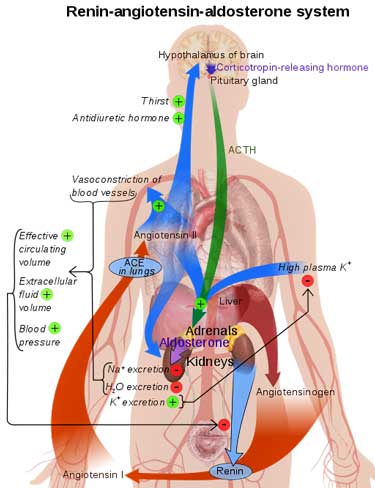
The renin-angiotensin-aldosterone system that regulates blood volume presents a paradox in ME/CFS and FM.
Renin is the first leg of the renin-angiotensin-aldosterone system (RAAS) that’s designed to deliver optimal blood volume levels. If blood volume is low, renin activity should be high.
First, renin stimulates angiotensin II, which increases blood pressure and stimulates sodium absorption. Angiotensin II then stimulates the production of aldosterone – the main factor – which regulates blood pressure, plasma sodium and potassium levels and blood volume. (Aldosterone secretion can also be stimulated by potassium, adrenocorticotropic hormone (ACTH), and low sodium levels in the blood (hyponatremia).)
Given the “profound” low blood volume found, both renin and aldosterone levels should have been dramatically increased, but the opposite was happening; they were both decreased in postural orthostatic tachycardia syndrome (POTS). With that, the “renin-aldosterone paradox” had been born.
The authors believed that reduced angiotensin levels were probably responsible, but also suggested the damaged autonomic nerves in the kidney could be a factor.
More surprises were in store.
The Ang II Surprise
In a 2006 paper, Stewart and Medow found that low blood volume was not universal at all in POTS. It was decreased in patients they called low-flow POTS, but not in two other subgroups.
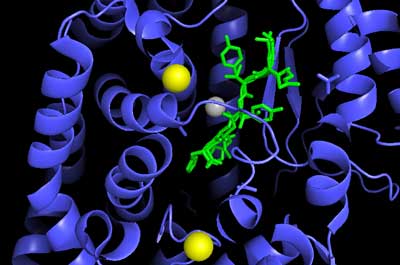
Angiotensin enzyme in conjunction with angiotensin. Very high levels of Ang II may be wreaking havoc in POTS and ME/CFS
The big news, though, was that instead of having low Ang II levels, the low blood volume and low-flow POTS patients had dramatically increased Ang II levels (2-3 times normal), as well as low renin levels.
Angiotensin II does more than increase blood volume. At high levels it can have some decidedly negative effects. Ang II ramps up vasoconstriction (narrowing) in the blood vessels by prompting the release of norepinephrine from the sympathetic nerves. It also jacks up oxidative stress levels through the formation of the superoxide radical and ultimately peroxynitrite. Increased peroxynitrite, then, can reduce the levels of nitric oxide – an important vasodilator.
High Ang II levels potentially set the stage for a ramped up fight/flight system, narrowed blood vessels, inflammation and possibly reduced blood flows to the brain. Since Ang II acts like a neurotransmitter in the brain, it could have multiple effects there as well.
Narrowing of the blood vessels (increased vasoconstriction) caused by Ang II could itself cause low blood volume simply by reducing the total volume of the blood the vessels could carry. The body senses the amount of space available in the blood vessels and seeks to provide the correct amount of blood. It might simply be providing the amount of blood needed to fill the reduced blood vessel capacity that was present.
High Ang II levels also appear to be responsible for the defects in the vasodilation in the small blood vessels in the skin, which sometimes cause acrocyanosis (bluish color) in the hands and feet.
There was another twist as well. With all that sympathetic nervous system activity going on, the low blood volume POTS patients should have high blood pressure – instead, they often have the opposite.
ACE-2 Enzyme
Five years later, a deeper dive into the renin-aldosterone paradox produced more answers – and more questions. In “Abnormalities of Angiotensin Regulation in Postural Tachycardia Syndrome“, Vanderbilt researchers suggested they’d found a reason for the high Ang II levels – reduced activity of the angiotensin converting enzyme 2 (ACE-2) that breaks down angiotensin. That was a timely finding as the ACE-2 enzyme had only been discovered seven years earlier.
Levels of the ACE-2 enzyme appear to be low in ME/CFS and POTS
The ACE enzymes (ACE and ACE-2) break down angiotensin in different ways. The first ACE enzyme (discovered in 1956) breaks down angiotensin into angiotensin II and angiotensin.
ACE-2 has been referred to as the “protective arm of the renin-angiotensin system“. It breaks down angiotensin to angiotensin (1-9) and angiotensin II into angiotensin (1-7). Basically, it protects against high Ang II levels being present. Plus, in contrast to Ang II, ACE-2’s end product, angiotensin (1-7), opens up the blood vessels (i.e. is a vasodilator). The low levels of Ang (1-7) found in this study suggested that ACE-2 enzyme activity was low.
Note that ACE-2 also cleaves or breaks up other peptides including bradykinin.
The authors suggested two reasons ACE-2 levels appeared to be low: (1) high Ang II levels; or (2) negative feedback from the low blood volume. (Low blood volume should prompt a reduction in ACE-2 – increasing Ang II – and then aldosterone – the main blood volume enhancer.)
Another Ang II Problem Crops Up – Impaired Baroreflex Sensitivity
The Vanderbilt researchers didn’t waste any time. The very next year, in Altered Systemic Hemodynamic & Baroreflex Response to Angiotensin II in Postural Tachycardia Syndrome, they investigated the impact of high Ang II levels in POTS patients.
They infused Ang II into POTS patients and healthy controls. As suspected ,the healthy controls responded to the increased Ang II with increased blood pressure: the POTS patients, however, did not.
That suggested that Ang II receptors lining the smooth muscles of the blood vessels were simply not responding well in POTS and that the desensitization hypothesis might be correct.
Interestingly, the study found that Ang II was, on the other hand, doing its job of retaining sodium. That indicated that problems with sodium retention were not causing the low blood volume seen in many POTS patients.
Then they found another possible high Ang II-related problem – a balky baroreflex sensitivity response. The baroreflex response refers to the rapid changes seen in heart beat intervals when blood pressure changes. The heart should, in a matter of seconds, alter its beat in response to any changes in blood pressure. The diminished baroreflex sensitivity seen in the POTS patients was strongly correlated with increased Ang II levels. Since the baroreflex response impacts the heart rate, the researchers proposed that high Ang II levels likely contributed to the excessively high heart rate seen in POTS during resting and standing.
The findings suggested that the Ang II levels were having various effects: blood pressure was not being regulated normally, and the heart rate appeared to be affected. Sodium retention, though, was fine.
The cause of the ACE-2 inhibition – the putative cause of the high Ang II levels – was unclear. The authors speculated that genetic mutations might play a role, but then introduced a strange possibility: they might not be measuring Ang II at all; but might be measuring Ang 3 or 4. Perhaps Ang II levels were normal, but Ang III or IV levels were increased.
In 2018, the same Oklahoma team that uncovered the presence of adrenergic and muscarinic autoantibodies in POTS found autoantibodies to ang II receptors in a small study. They believe these antibodies stimulate Ang II receptor activity and thus increase Ang II levels.
The Gist
- The renin-angiotensin-aldosterone system regulates blood volume in the body.
- People with ME/CFS and/or postural orthostatic tachycardia syndrome (POTS) tend to have low blood volume.
- When low blood volume is present, the activity of the renin-angiotensin-aldosterone system should be increased. In what has been termed the renin-aldosterone paradox – renin and aldosterone levels are decreased in ME/CFS and POTS.
- Low levels of some forms of angiotensin suggest that levels of the ACE-2 enzyme – which has been called the protective arm of the RAA system – are decreased. The ACE-2 enzyme breaks down Ang II and other peptides including bradykinin (see next blog)
- High levels of Ang II can increase sympathetic nervous system activity, produce systemic vasoconstriction (narrowed blood vessels), increase the heart rate, inflammation and oxidative stress.
- Miwa believes the low aldosterone levels may be caused by a balky HPA axis in ME/CFS. At the end of the day, though, the cause of the renin-aldosterone paradox and the low blood volume in ME/CFS/POTS is unclear.
- The SARS-CoV-2 coronavirus enters the body through receptors for the ACE-2 enzyme. Recent research suggests that many, if not all of the coronavirus’s effects, could derive from its disruption of the renin-aldosterone-angiotensin system and its failure to properly regulate a substance called bradykinin
- Two years ago, Wirth and Scheibenbogen proposed that bradykinin plays a major role in ME/CFS. The next blog will explore whether a similar bradykinin storm is present in COVID-19 and ME/CFS.
Chronic Fatigue Syndrome (ME/CFS)
The renin-aldosterone paradox had not gone unnoticed in chronic fatigue syndrome (ME/CFS) – which also features low blood volume. In 2014, Miwa found normal plasma renin, but lower aldosterone levels in ME/CFS, and declared that a similar renin-aldosterone paradox was present in ME/CFS.
In 2016, Miwa found low plasma renin activity, low aldosterone and low antidiuretic hormone. This time, Miwa linked the low renin-aldosterone activity to impaired brain functioning – specifically, reduced HPA (hypothalamus-pituitary-adrenal) activity. Aldosterone is produced by the adrenal glands.
Pointing to other HPA axis problems in ME/CFS (low cortisol, insufficient responses to corticotropin-releasing hormone and adrenocorticotropic hormone challenge tests), Miwa asserted that a blunted HPA axis was likely responsible.
In doing so, Miwa showed a way to link high Ang II levels to blood vessel vasoconstriction and inflammation, and low aldosterone levels. As high Ang II levels were jacking up the fight/flight system – clamping down on the blood vessels and producing inflammation – they were failing to promote aldosterone release from the adrenal glands because of a balky HPA axis.
(Miwa also found that providing desmopressin, an antidiuretic which reduces the amount of water excreted in the urine, eliminated orthostatic intolerance during a standing test, and improved stroke volume (amount of blood pumped by the heart), and significantly improved daily living scores in 5/10 patients with low “urinary osmotic pressures” in the study.)
Treatments for the Impaired Renin-Angiotensin-Aldosterone System seen in ME/CFS and POTS.
Treatments help some and not others, and can come with side effects. Remarkably few studies have been done given how often some of the drugs are used in POTS. Possible treatments include:
- Fludrocortisone (Florinef) – an aldosterone enhancer that increases sodium and water retention – Find out more here.
- Desmopression (DDAVP, Stimate) – a synthetic analog of arginine vasopressin that increases intravascular volume.
- Erythropoietin – a hormone that increases blood volume.
- Saline Infusions – increases blood volume – find out more here.
- Oral rehydration solution (WHO formula) – increases blood volume – find out how here.
At this point, much remains unclear.
It’s clear the renin-angiotensin-aldosterone system (RAAS) that regulates blood volume is messed up in ME/CFS and POTS, and is likely causing the low blood volume there.
Low, instead of high, plasma renin and aldosterone levels in the face of the low blood volume found has led researchers to term this situation “the renin-aldosterone” paradox in POTS and ME/CFS.
Two studies suggest that the activity of the ACE-2 enzyme is reduced (but it’s possible that Ang II levels are not being accurately assessed.) It’s not clear why ACE-2 activity is reduced, but genetic issues or low blood volume could account for it.
The low aldosterone levels remain the biggest mystery – and the biggest problem – since aldosterone is the main blood volume enhancer in the body. Given the low blood volume and high Ang II levels found in ME/CFS/POTS, aldosterone levels should be sky-high but are low. Miwa believes that a blunted HPA axis (aldosterone is produced by the adrenal glands) could account for the low aldosterone levels, but the cause is still unclear.
The high Ang II levels could be contributing to/causing the increased sympathetic nervous system (fight/flight) activity, narrowed blood vessels, the low blood volume, and inflammation.
Drugs and other treatments can help some people with the renin-aldosterone paradox, but can come with side effects.
*Please note that other kinds of POTS exist which do not produce low blood volume or problems with RAA system.
Conclusion
The renin-aldosterone paradox in ME/CFS and POTS has confused researchers for years
Why the focus now on the agonizingly complex renin-angiotensin-aldosterone system in ME/CFS and POTS? A system that has unresolved problems and no answers?
This is a setup blog to prepare for the next blog or two. Those blogs will cover an intriguing possible connection that’s shown up between ME/CFS and COVID-19 which features the same renin-angiotensin-aldosterone system this blog focused on.
A lot of thought is now being aimed at RAA system, and in particular, a “messenger” called bradykinin. Bradykinin, to my knowledge, has never been thought to be a major player in ME/CFS – that is, until 2018, when Wirth and Scheibenbogen pegged it as a possible major player in ME/CFS. Could COVID-19 already be informing us about what’s happening in ME/CFS and POTS? Time will tell.
Coming up next: RAS and Bradykinin – Where COVID-19 and Chronic Fatigue Syndrome (ME/CFS) Meet?
Hi Cort,
Thank you for this excellent, thought provoking write-up. I’m left a little perplexed, and hoping that chapters 2 and 3 might answer a few questions.
I have a high blood pressure version of POTS, with low aldosterone, inadequate response on an ACTH student test, adrenergic and muscarinic antibodies that have been linked to POTS and cerebral hypoperfusion.
So, I’m following everything you’re saying with interest. Some questions that are coming to mind are:
1) What impact does the fairly common ACE deletion have on these dynamics?
2) is there a diagram showing the interplay between the various elements in the system and what goes up when something else goes down? For those of us who are visual learners, that might be extremely helpful – maybe it’s in one of these papers that you’ve mentioned, but I haven’t seen it yet…
3) Exactly how do the antibodies interact with the biochemicals you mentioned?
4) And, aside from the drugs you’ve mentioned, What would playing with the other pieces of the system do?
I asked the last question because I recently added a drug called Kuvan to my protocol, which has had a dramatically positive effect. It increases tetrahydrobiopterin (BH4) part of Martin Pall’s discussion of the vicious cycle of peroxynitrite production, which works with folate, B12, and C. I believe this drug has helped to increase nitric oxide levels. My doctor had me get nitric oxide test strips from either Humann for Berkeley life, and I found that my NO tends to run low, and peroxynitrite production tends to run high. Adding Kuvan and/or the nitric oxide boosting product as quickly raised my NO level to optimal, and I’ve been able to reduce peroxynitrites over time using these strategies. And, this has lowered my blood pressure. It’s not a cure, because the second I don’t take these things the issues return, but they’ve done enough to show me that these are indeed part of the dynamic. I also take a beta blocker and Huperzine A, So these effects I’m getting by increasing nitric oxide are on top of the help I am getting from those.
(Apparently, LOW NO can lead to high peroxynitrites and a lot of other health problems.)
I’m really thankful that you are delving into this, because it’s a meaty topic, and I think that intention to it can allow patients to function better. Obviously a cure would be better, but understanding the dynamics of the situation, what tests we patients can have our doctors run, and the array of potential treatments that can intervene positively at various points in this complex system have the promise to give many of us back some function by reducing these debilitating symptoms.
Thank you and keep up with the good work!
Wow…I’m just learning about this but from what I’ve learned you have quite a combination there. Low aldosterone – low blood volume, low ACTH, if I have it right, could mean an inadequate response to Ang II (and therefore low aldosterone).
The Ang II antibodies are in the same “family” as the adrenergic and muscarinic antibodies linked to POTS – which is one reason why the Oklahoma team looked for them and found them. (More studies are needed to validate that finding). Perhaps the fact that you have the others suggests that you have the Ang II as well.
With all this new stuff in my head I can’t remember what the adrenergic and muscarinic antibodies do – except that they affect the blood vessels – probably squeeze them – and the heart rate as well as probably other things.
The ACE II is one possible reason that Ang II is – causing sympathetic nervous system activation and others but ACE II also breaks down bradykinin.
The high peroxynitrite/low NO levels make sense as, if I remember correctly, high Ang II levels can do precisely that.
I wish I had a visual diagram. There are lots of interconnections here – many more than I can sum up which I’m sure will pop up in the following blogs.
This is indeed a meaty topic!
Hi Cort… yes HPA Axis and ANS dysfunction clearly evident in ME/CFS. And my proposal is neuorinflammation of the hypothalamus (+ limbic system) might cause that and help account for the wide range of symptoms in ME/CFS… BUT my model also proposes an (inflamed) dysfunctional hypthalamic paraventricular nucleus (PVN), which is known to regulate heart rates and blood pressure… so I think the generally lower blood pressure found in ME/CFS could be related to an inflamed/ dysfunctional PVN, and lower blood pressure would then account for orthostatic intolerance (feelin dizzy when standing up), as blood would flow to the brain slower than required and exacerbated upon standing up). My blood pressure is alway lower during a relapse/ flare-up/ PEM (100/70), but normalises over time (120/80) as the perceived inflammation (headaches, aches, brain-fog etc.) and related symptoms (cognitive, gut, mood) dissipate… i.e. PVN (hypothalams) is key.
A neuro-inflammatory model can explain the onset, symptoms and flare-ups of myalgic encephalomyelitis/chronic fatigue syndrome (2019)
https://www.publish.csiro.au/hc/pdf/HC19041
cheers
Angus
Thanks Angus. It was so interesting to see Miwa pop the hypothalamus in there. None of the research done in POTS mentioned that possibility.
For those who are interested here’s a blog on Angus’s hypothesis
https://www.healthrising.org/blog/2020/05/27/neuroinflammatory-paradigm-chronic-fatigue-me-cfs/
My having POTS, ME/CFS and other things and knowing my subset type of POTS is HyperPOTS, I have higher blood pressures. We also found in my testing at Mayo that I have low blood volume and very, very low renin and aldosterone. Normally this combination is treated with high doses of diuretics. This could NOT be done with low blood volumes and POTS. The nephrologist told me that with these being near nonexistent in me, there was no way I would have high Angiotensin as that is between renin and aldosterone in the kidney pathway.
So, I did tons of research.
Appears the heart, brain and liver also produces Angiotensin.
Now think of this; COVID is going in on ACE2 receptors. It is also attacking the heart, brain and blood vessels. Where is Angiotensin produced…..heart, brain, liver and kidneys. The major filter organs, kidney and liver. The brain and heart affected. And as you pointed out it clamps down the blood vessels and with COVID there are blood clots.
My guess is my having low to no Angiotensin at my kidney level may be a protection for me. So maybe one of my wonky dysfunctions may save me a bit on this one.
But that makes me wonder about those on ACE inhibitors for high blood pressure.
The research I did way back when is on another forum for POTS. If anyone is interested, I can paste the links. I haven’t read it in awhile and I’m sure there is more known than back then.
BUT, I was also NOT to up salt and the drug Florinef, normally used for low aldosterone and to help the kidneys retain salt and up the fluid volumes, was a horrible idea for me. The kidney doctor suggested strongly for me NOT to do this.
We really need to know our WHYs and our subset types. If we don’t have the whole picture, we could mess ourselves up even more. Despite most POTS people trying to constrict their veins, I need to vasodilate mine….but only to a certain level. And, I also have too thick blood and that too is helped by vasodilating veins and using enzymes.
This is a deep subject Cort and a lot of complex connections. Good write up. I enjoyed it!
Issie
Cort, I sent you those 6 thread links from the DINET site. See if any of that would be helpful.
Issie
Issie,
I also have HTN. Currently on nifedipine,
carvedilol, losartan (got an ACE cough). I also take Lasix 60 mg daily for Meniere’s Dz so no other diuretics. I drink about 64 oz of fluids daily.
I live about 2 hours away from Rochester. I told my doc I wasn’t interested in a Mayo workup as long as they were still pushing GET and CBT as treatments. Now I see they have taken that off the main treatment recommendation page.
When and where were you diagnosed? Would you advise a workup there now?
I was DX at Mayo in Arizona. I’m not sure of the doctors in MN and how they evaluate there. The Mayo AZ is very through. They are pro medicine however, and I am not. I was DX with POTS, EDS, MCAS, FMS and other things back in 2009, if I remember correctly. Though all of these, to varying degrees, has been a lifetime thing and is in generations of my family. I wonder where EDS and FMS has its separation. But didn’t get official DX until then.
My ME DX came later. My sister and I both were in the Dr. LIGHTS study on families and mitrochondria issues and checking genetics.
I would also say that in my case, I found Mayo AZ doctors to be excellent to get a DX and have a through evaluation. However, they seemed to prefer treatment to come from your local doctors once that DX is made.
I personally prefer Functional Medical Doctors and trying to get the body to work more correctly, than masking with prescription medicines.
Thanks for sending the threads. Your nephrologist missed the renin-aldosterone paradox I guess. High Ang II levels can really pack a wallop.
On aspect of the high Ang II levels are low Ang 1-7, I think it was, levels. Ang 1-7 is a vasodilator! If you have low Ang 1-7 a vasodilator makes sense, at least to me.
I agree – this is such a complex subject – with a lot to learn and a bunch of different possibilities. We obviously need much more research.
Given the role the RAAS could play in ME/CFS it seems strange that only Miwa in the recent past has taken it up.
He was looking at it from purely a kidney level. Not taking into account it could be produced in other places. And at that time, there was little testing for it, as far as I remember. I did ask him however as the idea of high Angiotensin had been talked about among our POTS community.
But remember these ideas were brand new back then. The discovery of new subsets with POTS was just being established and defined. We were all in the beginning of discovery. And few knew that some of our subsets could NOT be treated the same. (And some still don’t know.) They tried to put us all on the same medicines and heavy salt loading. That was so, so wrong for me. (As you can see, from my post so long ago, I did not see this to be the correct way to go and was a bit verbal about it. I still hold to my opinion and hypothesis.)
Several things I questioned. Ideas I brought up to doctors. They got tired of hearing……”but Issie says”. (I had a doctor tell me that.) Also had a doc to bring in more help on one of my ideas with MCAS. Sooooo, pays to not go with the flow sometimes. A little push back and asking WHY and HOW COME. We get to new science and more answers.
Issie
Issie, According to an NIH article I read, ace inhibitors target ACE1 whereas ACE2 are insensitive to the actions of ace inhibitors.
I did an internet search and it appears still all over the map as to whether they think ACE or ARB inhibitors increase or decrease risk of progressive affects of COVID. Since those who need to be on them are at higher risk already, that is being speculated too.
Early reports said that they did feel ACE and ARBs up the ACE 2 receptors. However, some of them do increase potassium and that had been thought to be of benefit in the virus.
Appears some think it gives protection, others quite the opposite. One report suggested people switch to Calcium Channel Blockers.
One thing to note with these reports is if those reporting have an interest in the outcome or a change or continuation of said drug.
I can’t give advice one way or the other. Certain medical conditions require intervention with pharmaceuticals. That would need to be a discussion with ones own medical doctor as to what to do and the risk or benefits from treatments.
Issie, do you think it is possible that those with high blood pressure have many more ACE1 receptors than ACE2 receptors and that the inhibition of the function of the ACE1 would not necessarily affect the ACE2 and having less ACE2 would give some protection from SARS-COV-2?
@Tricia, one needs to study the trickle down affect of receptors and how they affect the receptors down the path. One will affect the other and either increase or decrease what it is supposed to affect……if it is working correctly.
It is all a big orchestra with many instruments. If one is off key, that affects the sound and tune of the whole group. There is still music, but it isn’t in harmony.
The goal is to have all those receptors tuned in key and working to moderate each other at proper tone, in harmony. Some receptors in the body upregulate and others down regulate. And this is along the same pathways.
The doctors and scientists who are studying this, are still uncertain the affect. There is debate as to how the angiotensin in different organs is affected. Should it be in the lungs, kidneys, heart, etc. And a possible difference between age groups, children vs. older adults.
So if they are uncertain the cause or effect, I surely cannot speculate on it either. Good questions however, I guess time will answer that one.
Thanks for the comprehensive reply, Issie. My husband is on ace inhibitor which Is why I am interested. He has high BP whereas mine is low so I dare say he is more likely to get Covid but have it less severely and I am less likely to get it but will have it more severely if I get it. So far here in Western Australia we have no community transmission as we are isolated from the rest of Australia with our border closed. I hope you are keeping safe.
@Tricia, Not sure that helped you much.
Hard times for the whole world, lots of unknowns and waiting to see. So far we are okay. Thanks for your well wishes.
Everyone, stay safe!
This was just sent to me. Talks about COVID and RAS and ACE inhibitors. Is an interesting, but a bit scary read.
https://elemental.medium.com/a-supercomputer-analyzed-covid-19-and-an-interesting-new-theory-has-emerged-31cb8eba9d63
Very interesting article. Thanks, Issie.
Interestingly I’ve tried 3 of the 5 listed treatments and suffered intolerable and overwhelming fatigue with all 3. For some reason my body objects to me pushing in that direction.
I think this is not that uncommon. So many paradoxical reactions – which to me shows that this system is involved but that we’re missing pieces…
Can’t wait for your next blogs, Cort! I remember you wrote about the RAAS system being implicated in ME/CFS a while ago. Do you mind providing a link for that?
So looking at Bradykinin, evidently having it dis-regulated can increase pain and inflammation. Apparently it can operate similarly to histamine and cause problems like sinusitis (common in us with ME/CFS and I’ll bet it might be an underlying factor in mast cell problems in Ehlers-Danlos where POTS and other autonomic problems are so prevalent). It’s also linked to inflammatory cytokines although I haven’t checked which ones it mostly influences–but then again there is a lot of differing results in ME/CFS studies. And there is also a link to autoimmune disorders and more…
So, even though Bradykinin has a very brief half-life (17 seconds!), it appears to be very powerful–it has to be to regulate HR and BP. So what can regulate Bradykinin? Monoclonal antibodies. They are currently being used in a wide array of conditions including autoimmune disorders and cancers. Looks like they are being considered for Covid treatments too.
This makes me wonder if anyone has tried them for ME/CFS yet. Perhaps I am overlooking the classifications of some of the drugs already tried for chronic fatigue. Well, every new tidbit of information is a tidbit of hope!
Hi Nancy,
I‘ve been intrigued by Bradykinin as we’ll as I was checked for MCAS (have POTS, ME, pain and some allergies). Turned out that I don‘t have high histamine-mediators. Antihistamine-drugs do nothing for me… BUT: cromoglicic acid! It‘s like a game changer – more stamina, no Brainfog, less potsy). I was very confused and them I discovered bradykinin that acts- like you are saying – like Histamine. But it’s not a mastcell-product. Hm. Than I read that apparently Cromoglicic acid does not only have an impact on mastcells, but on other mediators as well- like kinines. So I‘m extremely intrigued by all these theories popping up again with covid. The mechanism behind Cromoglicic acid Is not clear
although the drug has been known for decades…. so yes Bradykinin seems to play a key role. All the best.
So interesting Nancy! Thanks for passing that along. Bradykinin is indeed an fascinating substance.
I don’t remember by RAAS blog -which doesn’t mean anything – I forget blogs (lol_. I’ve actually kind of avoided this system as its so complex but jeez – here we are with low blood volume and no real answers for it.
Thanks for the info on bradykinin. It’s short half life makes it hard to measure = but one researcher is doing that in COVID-19. The link to histamine and mast cells is really intriguing.
Talk about leaving us on a cliff hanger Cort! As RAAS function also has role in diabetes and diabetic heart disease, solving this mystery cld have wide ranging impacts. My mum’s adrenal glands collapsed (part of Schmidt Syndrome) and I have hypovolemic POTS…so I’m not surprised to see Aldosterone link.
You’ll probably like https://diabetestalk.net/blood-sugar/how-is-cotransport-used-to-move-glucose-into-the-intestinal-epithelial-cells
Tittled “How Is Cotransport Used To Move Glucose Into The Intestinal Epithelial Cells”
“In glucose absorption, there is an initially high concentration of glucose in the lumen of the gut as carbohydrates break down. This means there is a concentration gradient allowing the diffusion of glucose into the cells. Once the glucose is at equilibrium, it then needs to be taken up by active transport: 1) Sodium ions (Na+) are actively pumped out of the cells of the small intestine and into the blood via Sodium/Potassium (Na+/K+) pumps. 2) This creates an Na+ concentration gradient, where there is a higher concentration of Na+ in the lumen of the small intestine than inside the cells. 3) The Na+ then re-enters the cells of the small intestine via diffusion through a sodium-glucose transporter protein (alongside glucose). 4) The glucose concentration inside the cell increases and a concentration gradient is created between the inside of the cells and the blood. This allows glucose to move via facilitated diffusion into the blood.”
It remains difficult science, but (If I made no mistake) step 1 says:
Sodium is pump out of the gut epithelial cells into the bloodstream. This pumping is done using no ATP but potassium taken away from the blood stream. That then leads to glucose uptake.
That “taking potassium out of the bloodstream” is a strong driver to force the renin-ACE2-aldosterin system in another direction to protect the vital potassium/sodium blalance, potentially leading to many symptoms downstream for a whole range of nasty disseases. The potassium part is very often neglected in science as “most often” it’s not problematic.
Why does it play a role in our diseases when everybody has those co-transporters? Because IMO the gut can also use ATP as an alternative driver for glucose and or sodium uptake. If ATP is short…
Please just don’t mess around with potassium just yet! Read the bigt warning in my post below.
When seeing the upper picture of the body and those relationships between those chemicals, one thing sprung out: the effect on potassium!
I remembered from blood test that my sodium values are always high-ish but within margin and my potasium levels are not. That is while still using rarely any salt on my food safe for the salt that is present in what I bought.
I also remembered that the balance sodium to potasium is related to heart rate, irregular beating and potentially heart / chest pain.
=> When looking at that figure, I saw the zone with
Na : (-)
H2O : (-)
K : (+)
=> RENIN HAS OPPOSITE EFFECT ON SODIUM AND POTASSIUM!!!
When digging further, all points to our bodies scrambling to hold on to a reasonable sodium potasium balance.
Again, due to WordPress blocking too many links, I’ll describe the links otherwise:
* Site from doctor Kara Fitzgerald:
“Low serum potassium in COVID-19 and thoughts on interventions”
(relationship: COVID-19 is related to high ACE2 levels)
* A paper from “Alexis A. Gonzalez,1,* Matias Gallardo,1 Carlos Cespedes,2,3 and Carlos P. Vio2,3”
Titled “Potassium Intake Prevents the Induction of the Renin-Angiotensin System and Increases Medullary ACE2 and COX-2 in the Kidneys of Angiotensin II-Dependent Hypertensive Rats”
(so too low potasium (intake, retention) likely would reduce medullary ACE2)
* webiste(healthline), blog “8 Signs and Symptoms of Potassium Deficiency (Hypokalemia)”
“1. Weakness and Fatigue
2. Muscle Cramps and Spasms
3. Digestive Problems
4. Heart Palpitations
5. Muscle Aches and Stiffness
6. Tingling and Numbness
7. Breathing Difficulties
8. Mood Changes”
=> Now we have at least the first 7 clearly being part of our conditions. Imagine if ACE2 and renin increased: potassium levels should drop considerably and make all 8 of above symptoms clearly worse. Starting to see a pattern?
* website(Livestrong) has a blog on “Rapid Heart Rate & Potassium”
“Levels of blood potassium vary inversely with heart rate; as the levels of potassium drop below normal, the heart rate increases beyond normal.”
(personal note: many believe the ratio between potasium and sodium is as important as the absolute amount of potassium to many effects)
* A paper in pubmed Titled “[Effects of potassium on renin and aldosterone]”
from “T A Kotchen”
“The renin-aldosterone system contributes to the regulation of arterial pressure and to the maintenance of sodium and potassium balance. Alterations in plasma potassium concentration have opposite and independent effects on renin secretion by the kidney and on aldosterone secretion by the adrenal gland. Renin secretion tends to be inhibited by hyperkalemia and stimulated by potassium depletion. In contrast, increases of plasma potassium directly stimulate aldosterone secretion. This effect of potassium on aldosterone serves as a protective mechanism against the development of hyperkalemia. Conversely, hypokalemia inhibits aldosterone production. Small changes in plasma potassium have a greater effect on aldosterone than on renin secretion. In patients with essential hypertension, diuretic induced alterations in serum potassium concentrations may affect both renin and aldosterone secretion.”
=> Again: renin and aldosterone have an opposite effect on potasium and sodium and renin and aldosterone are regulated the opposite way when dealing with high levels of sodium versus natrium; also: balance between both is important.
* Another pubmed paper titled “Role of the renin-angiotensin system in potassium control” from “D B Young, R E McCaa”
“To determine the importance of the renin-angiotensin system in control of plasma potassium concentration and excretion…
The sodium forcing did not result in measurable changes in plasma potassium concentration or excretion in group I, in which PRA fell to 40% and plasma aldosterone concentration (PAC) (dejurgen note: plasma renin activity) to 60% of the low sodium levels. In group II (dejurgen note: with faulty renin system) the same sodium forcing produced a 12% decrease in plasma potassium concentration and a 79% increase in urinary potassium excretion.
The results demonstrate the importance of the renin-angiotensin system as a link between the nephron and the zona glomerulosa that is essential in controlling plasma potassium concentration and excretion during changes in sodium balance. ”
=> When “force feeding” healthy dogs a high sodium diet, dogs with an intact renin system did keep potassium levels and excretion constant, dogs with a faulty rening system wasted their potasium”
=> Another sign IMO that our renin system wants to keep our potasium and potassium versus sodium balnce intact even at (?a very high?) cost.
* Looking at Corts recent blog on (Oral Rehydration Solution More Effective than Saline IV at Improving Orthostatic Intolerance), researchers did find:
* ORS was better then IV saline in several aspects.
* “oral saline” was bad and did increase edema rather then blood volumes.
* wikipedia(Saline_(medicine)): it contains only sodium, no potassium
* ORS: also potassium in it
=> Saline lacks sodium, ORS has potasium giving clearly better results according to Cort’s blog.
* Modern food is often sodium loaded, not potassium loaded (even for those taking care of maximum sodium intake like I naturally / instinctively tend to do)
* The ORS blog of Cort pointed to the “intestinal Na+-glucose co-transport (GLUT2,symporter) carrier”. That carrier makes it easier for the gut to take up sodium if there is glucose present BUT also to take up glucose if sodium is present.
Now there does also exist something like a Sodium-Potasium Pump, see wikipedia(Na K ATPase). That imports 1 sodium ion and exports 1 potassium atom simultaniously. This form of ion transport has the advantage of not costing (at the place of use) any ATP. Those Sodium-Potasium Pumps are used wildely troughout the body, including in the gut next to the before mentioned “intestinal Na+-glucose co-transport (GLUT2,symporter) carrier”.
=> It is rather complex, but the “intestinal Na+-glucose co-transport (GLUT2,symporter) carrier” can therefore work togeter with those Sodium-Potasium Pumps to import glucose from the gut into the blood stream by dumping potassium from the blood stream into the gut.
=> For our often energy (and blood flow) depleted gut, importing glucose without needing ATP can look attractive. Both importing glucose by co-absorbing sodium AND importing glucose by dumping / wasting potassium can be done without the need to use ATP in our guts.
See website(diabetestalk), blog “How Is Cotransport Used To Move Glucose Into The Intestinal Epithelial Cells”, third picture above the subtitle “What Is Active Transport And How Is It Used In The Absorption Of Glucose?” to explain it a bit better. There are better figures available on the internet, but with weird link names that will get this comment locked by WordPress.
note: when looking at the picture on the bottom of that blog with some more different co-transporters, ïf* I get it right Cl salt favor lower energy consumptium and decrease potasium waste. In the ORS K+ is such salt just like most of the Na+ salt. This is however complex so I need to recheck this one.
I wanted to be quick posting this before it gets snowed under by plenty of other coments, so the quality of references may not be optimal or there may have slept in some mistakes but I think the overal point will remain standing.
I think this is the first time I say that in a comment, but:
=> CONTRADICTION SOLVED?!?!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
NOTE: DON’T JUST GO AND BUY POTASSIUM SALT AND “SUPPLEMENT” TO OWN DESIRES: TOO HIGH POTASSIUM INTAKE CAN BE !!!!DEADLY!!!! AT THE VERY LEAST CONSULT YOUR DOCTOR FIRST!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
The above in more plain English:
The Renin-ACE2-Aldosterin system not only tries to maintain blood volumes, prevent edema or keep sodium levels in check. It seems, according to the links I did find quickly, to be “even more determined” to keep potassium levels and the ratio potassium to sodium intact.
From the webiste(healthline), blog “8 Signs and Symptoms of Potassium Deficiency (Hypokalemia)” this happens with too low potassium levels
“1. Weakness and Fatigue
2. Muscle Cramps and Spasms
3. Digestive Problems
4. Heart Palpitations
5. Muscle Aches and Stiffness
6. Tingling and Numbness
7. Breathing Difficulties
8. Mood Changes”
Note that the same AFAIK happens if the ratio potassium to sodium is too low.
That reflects in my bloodwork: normal Potassium levels and bordeline high Sodium levels. That seems perfectly fine. But think of how well those 8 symptoms above match part of our diseasses. Borderline low Potassium levels combined with borderline high Sodium levels would increase all of the above 8 sysmptoms in strength and we already have them pretty bad.
=> This could be a very clear showcase where “in range” hides a very bad problem in plain sight when having a certain condition. As research with the dogs linked above shows, the dogs Renin-ACE2-Aldosterin system is willing to take a really bad hit in order to keep potassium levels normal and to prevent potassium excretion in the urine.
Why could it be so (much more) important for us patients for our bodies to hold on so tight to potassium? Potassium can be used as a sort of “currency” to import sodium or glucose from our guts. That can reduce the need to use another major “currency” typically used to import sodium or glucose from our guts: ATP.
We are “starved” for ATP, our guts probably are even more starved for it as our typical fight-or-fligth response reroutes blood (and thus energy) away from the gut towards brain, skeletal muscle and liver. And ATP sure does cost plenty of energy to produce.
=> So, when our guts have to absorb an excess of sodium or need to absorb glucose from the gut, wasting / dumping potassium in the gut rather then using ATP as a currency sounds quite attractive. This however goes hand in hand with lowering blood potasium levels and lowering potassium to sodium levels.
I’ll repeat the warning in the summary:
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
NOTE: DON’T JUST GO AND BUY POTASSIUM SALT AND “SUPPLEMENT” TO OWN DESIRES: TOO HIGH POTASSIUM INTAKE CAN BE !!!!DEADLY!!!! AT THE VERY LEAST CONSULT YOUR DOCTOR FIRST!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Also, I’ll add one much needed thing: to thank patient-pioneer Issie when it comes to changing how patients and doctors alike look at POTS. Without your help I wouldn’t have gotten today to this conclusion. Thanks so much for all of us from the bottom of my heart!
Thanks as always Dejurgen. Potassium issues have not been dealt with in the papers I read either but potassium was listed as one of the stimulators of aldosterone. I had no idea about the possible ramifications…
I often wonder about “normal” ranges. There is normal for a healthy person but perhaps a different normal for someone who has ME/CFS…
So many factors! 🙂
Please feel free to post your personal blood levels of potassium and sodium to see if this checks out. Please name your related diseases with it.
Note: if it goes against these ideas, please do submit that TOO!
I’ll start:
ME/CFS; orhtostatic intollerance but no POTS
Potassium near always close to the middle with a mild tendency to be somewhat below the middle.
Sodium near always close to or at the upper limit with it never being below average.
ME, fibro, Meniere’s Dz, HTN, IBS
09/03/2020: K+–4.1 mmol/L(lnml 3.6-5.2); Na–140 mmol/L (nml 135-145); chloride–103 mmol/L (nml 98-107) Bicarb–29 mmol/L (nml 22- 29); anion gap–8 (nml 7-15); Ca–9.5 mg/dl (nml 8.8-10.2)
07/01/2020: K+–4.3; Na–143; chloride–103; bicarb 26; anion gap 14; Ca–9.8
04/17/2019: K+–4.2; Na–145; chloride–103; bicarb 29; anion gap–13; Ca–122
Thanks for volunteering to take a look!
Thanks for repyling.
I didn’t list my exact values as I expect half a dozen or more different units and “normal” ranges across the world. So adding normal ranges and units is a good idea.
Just being a numbers guy here, I’d say Na ranging from average (140) to max (145) too and K always a bit below average (4.4 here) too.
Anion gap has different ways of calculating, so without knowing which way, it’s not of much use I think.
The rest, I have few measurements of my own on. The result of test is just the same every single time: “we don’t see anything wrong with your blood values”.
Remember, I have no medical education whatsoever. I’m a patient that happens to be not half bad at connecting dots and puzzling.
I forgot to mention I have IBS (and bad fructose malabsorption) too.
Is that last Ca value 12.2? Wow.
AMEN!
On Issie’s contribution to the field and all of us.
♥ ♡ ♥(ꈍᴗꈍ)ε｀*)♥ ♡ ♥
. . . ･:*☆ ヽ(*⌒∇⌒*)ﾉ
***asgree*** with Meirav
Bravo Issie and Dejurgen and as always: Cort
my brain 🙁
***AGREE*** !!!!!!!! with Meirav
(hope Cort edits the first!!!)
My levels same as Dejurgen.
As a side note, upping potassium as a supplement or medicine (like in blood pressure medication that also ups potassium), was not a good remedy for me either.
What did help was upping foods high in potassium with all the assisting minerals in them.
Anyone else crave potatoes?
If that is a drug that also blocks the Na+/K+ exchanger, a likely way to reduce potassium excretion by the kidneys, then you take away that “emergency currency” from the body. Bad idea.
That Na+/K+ exchanger is vital in many processes throughout the body, including in neurotransmitter use. Blocking that when they are already disturbed: potentially a very bad idea.
Up Potasium too much and it WILL affect your heart (badly).
Up it in a single dose a day and chances are big blood potasium levels WILL SWING too much.
Up it to compensate for what is supposedly short and you might create normal blood flow and volumes reaching / flooding decades old inflammation zones. Bad idea. That’s like opening the windows and doors of a house with smoldering fire. Expect a huge ball of fire comming your way! Has to be build up (very) slowly and bit by bit. AND WITH DOCTORS GUIDANCE. MEDICAL CONDITIONS UPPING POTASIUM TOO MUCH CAN AFAIK BE DEADLY IN DAYS !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Ha!
Craving potatoes would be an understatement.
The way Tracey Anne as her chocolate and chocolate chip cookies –
I have potato chips (plus chocolate too, usually at the same sitting. They are maybe two of the very few manufactured products in my diet…)
It was potato chips that first tuned me on to potassium being relevant.
I slept very little one night, and had to go out during the day
and nerves abuzzing all over like they hadn’t in quite a while.
A bag of potato chips dialed it down to faint tingling.
Minerals seem to be affecting my nerves:
I had tried table salt before – as in adding a bit to salad – and that also sent my nerves bonkers, in a different way (touching them made them jump like a live wire).
Potato chips = sodium + potassium (in the right ratio for me?)
I think the relationship between potassium-sodium-magnesium-phosphore-calcium is telling. At least in me.
The first three – borderline low/low,
the other two mid-range normal.
My records only go as far back as 2007.
I get the sense my problem is that minerals are not getting to where they need to.
What regulates their transport into and out of cells?
And that brings me to taurine, putrescine… ALP doing something similar for B6… BH4? It’s hard to find the balance, with interventions in the 1-carbon metabolism.
I find something that works and soon it messes up balance of things.
It’s frustrating. I am now experiencing very high blood pressures, even in supine.
I’ve been trying for a few years to up magnesium with no results.
Same for iron. They don’t budge on the blood tests.
Before I knew them as POTS episodes,
since my teens – I thought they were brought on by dehydration
(as they tended to happen in the heat, summer months)
So I would counter them by eating potassium-rich foods.
bananas, peaches, tomatoes those who can.
Watermelon – I found out can make me really sick (can be because rich in citrulline and ups arginine in the body, it’s can vasodilator. A small slice I’m OK. A bit more, I found, does not bode well)
Michelle, the woman behind the MCAS website, drinks sodium/potassium bicarbonate mix daily as antihistamine, and found that it helps her POTS too
(she has hyperadrenergic POTS as well).
Her site hasn’t been up for a while.
The advice for that comes from Dr. Joneja, who specializes in histamine problems.
Here you can read about it a bit
https://www.alisonvickery.com/blog/natural-antihistamine%2F
It seems she doesn’t advice for it to be taken every day?
PROCEED VERY CAREFULLY
Baking soda is doing quite a number on my digestive system.
I’m not sure I can handle the mix well for now.
Right now, I’m having a really bad case of super high blood pressure, even in supine. I’ve also messed up my nerves some at times.
This is to illustrate the point Dejurgen and Issie wish to drive home:
.｡*ﾟ+.*.｡ .｡*ﾟ+.*.｡.｡*ﾟ+.*..
PROCEED WITH CAUTION.
SUPER CAUTION
SPRINKLES, start with SPRINKLES of substances and foods.
This is what SPRINKLES looks like:
-ˏˋ⋆ ̥
THAT’S how much – GRAINS
.｡*ﾟ+.*.｡.｡*ﾟ+.*.｡.｡*ﾟ+.*.｡.
Hormesis, homeostasis
tricky business in our line of work/health…
I have those low fat oven baked ribbled (quicker uptake) natural taste (just a bit of salt on them) chips I use as a “medical aid”. When opening them, it’s hard to not empty an entire family bag by myself. It took quite a bit of training to learn to “dose right and modestly”, especially when I open them when I crave them.
Such chips covered in chocolate? Madness. I don’t even consider buying those. That would be way too unhealthy as I’d fail to manage my intake. Let me add that I have a strong willpower to food and snacks that I like. I can say no to sweets, cake, candy, ice cream… when multiple people around me eat them with a smile on their face. And I do like to eat that food. I also eat modest amounts of food a day. But such chips covered in chocolate? Pure madness I say!
When looking back to my food preferences, many of those foods are high in potassium. That includes many (dried) fruits too. The combo sugar (glucose) with Potasium is a strong one when talking about this co-transporter. That was a craving I had till my diseasse turned for the worse. Bad fructose malabsorption problems learned me not too eat dried fruit.
Potatoes are not only rich in Potassium, their carbs also largely decompose into glucose (more then many other high carb foods). That plus the right dose of salt is playing in the cards of several different co-transporters.
Calcium, magnesium and phosphor are involved too. Our western food pattern, even if eating healthy, is very much lobsided towards sodium versus potassium however. One needs a specific diet to not have it or have it reversed.
(@Meirav: any chance you somehow eat a very low (total, prepared food included) sodium diet compared to average healthy people?)
It makes much sense this affects MCAS too, as low blood volumes do affect it badly to start with. Quick release of histamine is a big way to alter blood flow quickly. On top of it, the potasium sodium balance influences both neuro transmitters and IMO the endothelial cells of the blood vessels. Those co-transporters excell at quickly reacting to changes. Blunting their use by an upset potasium sodium balance might cripple that ability.
Making new ATP requires more time to adapt. Glycolisis reacts slow-ish but too slow. Adapting aerobic ATP production is way too slow to provide the endothelial cells the energy to constrict blood vessels when standing up.
So when standing up quickly whilst having an impaired potasium sodium balance reaction will be slow and the body will revert to a huge burst in anaerobic energy production. That fits the condition.
Too speed up this still too slow anaerobic ATP production, the body can release a strong burst of (nor-)adrenaline. That speeds up the anaerobic production of ATP quite a bit, at the cost of “going hyper” or all frenzied.
Consider this:
Ever tried to “fertilize” a farmers land and crops with kitchen salt (Sodium Chloride)? You’d be glad to make it out alive as the farmer would be very very angry for you poisoning his land and crops. But he pays big bucks for plenty of Potassium rich fertilizer.
We (at least those who are not medically forbidden to use kitchen salt) and the food industry? We do the reverse. Sprinckle the food with plenty of Sodium. Ever seen someone without a heart condition using Potassium salt on his food?
AND AGAIN: DON’T DIVE HEAD FIRST IN UPPING POTASSIUM!!!!!! See above big marked warnings!
never ate salt before—except rarely on raw potatoe slices and even more rarely on watermelon.
suddenly ate salt by the pinchful anytime before sleeping
( not table salt) and it tasted sweet. eventually turned ‘yuck’—-salty again……… then sweet again.
eating way more potatoes………….instant, baked, ……….
and salt butter…..
crave potatoe chips but avoiding them mostly—- may reconsider this now
Though we have had some fun considering eating potatoe chips, that may not be the best option. The fast frying in oil, not the healthiest. And then take into consideration that they are also a nightshade, and nightshade seem to make most FMS people hurt more. But, I still crave them. ……
There are other options to up potassium. So do a search for those foods. As I said earlier, I felt foods with all the assistance minerals, whole, complete foods was better than a supplement or a medicine.
Supplements of minerals and vitamins are very concentrated and usually too high in that concentration. The body has to process that. It becomes more of a medicine. I personally prefer herbals as Supplements and use non standardized. That way you get it more in its whole form. But the old saying of “let food be thy medicine”…. still is the best policy.
If this Na+ / K+ ratio would affect our blood volumes and health, REconsidering trying to increase blood volume with consuming “oral saline” or water with table salt and selecting some more healthy potasium rich foods plus having a modest food intake apears to be the better choice to me.
I do often have some bags of low fat potatoe chips at home for “in case”. When I am in need of comfort food they appear to have some advantages next to their disadvantages trumping many other comfort foods at that.
Them having net advantages requires IMO to consume only small amounts under strict circumstances and having a good body awareness to see *if* and when they help you.
Still, balancing that Na+ / K+ ratio with an optimal diet (taking into account food intolerances) AND pacing enough should make that “trick” largely of few use. When using it, I think it’s best to take the opportunity to drink some water to actually increase hydration rather then creating constipation.
Note: One size does not fit all. I for example drink a cup of weak coffe before sleep in order to sleep better… saying this to illustrate that point.
I have high blood pressure and my heart is usually in the 60s/low 70s. But if I go into a post exertional malaise, my heart rate goes up to high 80s resting, and spikes into 100s if I stand for a few minute and my blood pressure drops, so classic POTS, but only during PEMs. I got the high blood pressure before I got ME/CFS, and got a full adrenal workup, because the only med that worked was spironolactone, a potassium sparing diuretic that also acts on adrenal receptors. The adrenal workup didn’t find anything. But later, after I got ME/CFS, and years later after I REALIZED it was ME/CFS and stabilized with pacing, I thought I would try going off the spironolactone. BIG mistake! I started constantly going into PEMs. It was awful. And my blood pressure went up. So it is interesting to hear ideas around potassium, and the complexity of all the hormone interactions. I have to drink a LOT of water, big glass every hour to feel ok – maybe because of the diuretic part, but my blood pressure is always normal or a little high. Thanks for this Cort. Sooo complex. And thanks for the article about the WHO water. I got some for the next PEM round. Although it might be hard to get it down, since I get so nauseous and it doesn’t taste great. Hoping it helps, and for breakthroughs in POTs. 🙂
Thanks for sharing this Chris.
Having POTS only during PEM makes sense when looking at the (potential) role of potassium.
During PEM our response speed is even more sluggish then otherwise. And for many, including me, my base temperature then drops considerably. I had 34.5 °C measured the morning after my biggest crash ever when I was in hospital *on a very hot summer day*. That reading was dismissed as “impossible, it must be a broken thermometer”. The morning after that it was still only 35.5 °C. At first I was quite dissapointed they did keep using that defunct thermometer during an entire day and night (visitng many other patients) without replacing it.
During a functionality test I was brought by a wheelchair to the physical therapist’ room and had to walk a few meters along two bars supporting me. The first length I was able to do with plenty and plenty of focus and willpower. Going back in the other direction to my wheelchair was another thing. It probably took me 5 minutes to gather the strength, energy and courage to even attempt it. I was soooo weak and my limbs so shaking. When reaching my wheelchair I had my first major hyperventilation incident ant it was “amazingly memorable”.
I started folding completely up and down in that wheelchair and making loud noises in between wheeping and screaming again and again for 5 minutes. I had NO control over my body. It WAS going to do that and my will nor mind had NO say in it. It wasn’t emotional to me. I did not feel fearful despite it being a violent sensation, being displayed to half a dozen other therapists and patients in that room. I sort of “was that movement” and “that movement was survival”.
The next 5 minutes I slowly started to get some control back over my body. The entire episode lasted about 15 minutes. I felt no shame, despite it being a very weird “pathethically crying like” scene and there being two other therapists seeing it that I had visited for over a year and had a good (patient-caregiver) relationship with.
I left the hospital with “CFS flare up. nothing seen diagnostically.” reported. Well, if measuring hypothermia / impossible low temperatures is nothing :-(. Months later I realized I had this (a little bit less extreme) very frequently in the morning and could repeat measuring low borderline hypothermia temperatures every day. I actually “got it” after weeks of frequent “violent shaking my limbs with great force” that it was related to hypothermia. As I always felt cold-ish since being sick my sensation of having cold didn’t felt that out of the normal.
The shaking screaming hyperventialtion scene was “of coarse” discribed as an emotional induced thing. I can’t blame the neurologist for that one however as he didn’t experience what I did.
That episode holds many elements of what is described in the list with 8 points of things to go wrong when the potasium / calcium balance goes wrong OR when those co-transporters fail for another reason and the symptoms were, BIG, QUICK ONSET and OVERWHELMING!
Hmm, I’m wandering off. Such a low body temperature would go hand in hand with being (even a bit less then usual) able to do very few AND my “engines standing by running in idle” all failing and halting at once, making my reaction of mind and body very very sluggish and faltering.
So, during PEM you would in this hypothesis even more vitally depend on those NA+/K+ co-transporters.
The idea of slow blood vessel adaptation and with it the need (of the body) to use large amounts of (nor-)adrenaline also might hold to some amount to the brain.
Everybody with a bad case of ME will know how difficult it is to quickly react to changes or to think quick at all. Having a conversation that switches topics can confuse my mind. Thinking fast is waaaayyyyy more exhausting then thinking slower but taking my time to finish the problem. Being in a pleasing natural environment with slow changes is waaaaayyyyyy easier to my brain then quick busy traffic. That can crash me badly.
See the parallel? Quick changes in the way we think and observe require quick “micro” reactions of the blood flow in the brain. With a blunted potasium / sodium (and calcium too) balance those quick co-transporters wont be of much help. That’ll make “micro tuned” blood flow adaptation sluggish.
Worse, many neurotransmitters use those co-transporters as a way to react quickly AND likely as a source of “private / local energy reserve for each neuron”. So the neurons will likely react more sluggish too.
Knowing a bit of artificial (computer, electronics) neuronal spiked networks (that try to mimic the working of the brain) I know that both signal strength AND timing are important in those networks.
Blunt that co-transporter and you’ll mess with both. That should confuse our thinking, brain motion control, reaction to pain… quite a bit.
What *MIGHT* the body try and do in response: “keep the engines running hot”.
With that I mean: *increase* average “standy” energy / ATP production to be ready and available to use it any time when it is needed. That’ll keep us somewhat functional. We’ll be somewhat able to react “good enough” despite lacking a “quick start fuel”.
Compare it a bit with an old 1950’s army truck that you had to keep the engines running if you were planning to drive away quickly on a moments notice (as it starts up so slow) versus the modern cars with star-stop mechanisms to save fuel when waiting idle. They’ll stop and restart the engine in less then a second when waiting in front of a traffic light.
Now wasting all that energy is in line with some researchers saying ME is hypo metabolic (producing and consuming too few energy) and others claiming it is hyper metabolic (producing and consuming too much energy): we likely produce and consume too much energy for bein able to do very few.
All that “keeping the engine hot” comes at a cost:
* we use too much energy for the basic things we can do
* when not using that “stand by” ATP (and NADH, FAD, NADPH…) our cells continuosly make (in this hypothesis), what do they have to do with it? Wasting to it is but one thing that will happen. Producing but not using ATP, NADH, NAPDH… is an *excellent* way to produce plenty and plenty of ROS (not that we want that!).
Even despite the above disadvantageous, standing by “iddle” “keep the engines hot” aerobic (Krebbs cycle) energy production we still will need quick bursts in anaerobic (lactic acid making) energy production for every quick thought, jump between topics in conversation, visual overstimulation… further “poluting” our blood.
There is one more thing to be considered:
If I get it right part of “modulating / regulating” how the brain reacts to stimuli from our sense and how we react to thoughts and emotions *LIKELY* is done by (micro, precisely for each small indivudal brain region) regulating the flow of blood (and energy, oxygen with it) to each individual region.
If that idea AND the idea of “keep the engines running hot” both were true, then ALL brain regions not actually needed for a certain thought, visual impuls, pain impuls… but “keeping the local (cell / neuron / nerve fiber) engines running) will ract TOO STRONG disturbing thought process, pain sensing, emotional impacts, visual and auditive inputs… a lot making them (highly) “inacurate”.
That happens in ?all? of our conditions. Our brains “flaring up like a Christmass tree under a scanner” for doing simple actions like talking, thinking, looking at pictures, being pinched in the fingers… is so typical for us. In healthy patients the activation of brain regions is waaaayyyyy more focused to just activating the specialized brain.
Again: way more energy use, likely wa
oops, hit enter by accident (so glad I din’t lost this comment)
Again: way more energy use, likely way more ROS production for all that ATP, NADH, NADPH,… being needlessly produced, stacking up in the cells that don’t need it (that is a process known to create plenty of ROS) while being short in the cells that do need energy / ATP (as the during idle created aditional ATP / NADH… is set in between rest and action to be both quick-ish enough and consume reasonable-ish amounts of energy and producing only reasonably-ish amounts of ROS), incoordinated and inaccurate response of both brain and nerves to stimuli including pain and thoughts… all comming together in our diseases.
All of that topped by a dressing of stress hormones like nor-adrenaline as this strategy of “keeping the engines running” plus “using bursts of anaerobic energy production” isn’t fast enough for us to function anywhere near normal. This dressing with stress hormones is the needed corner piece to let this strategy work: it is very likely needed to make our anaerobic energy production kick in fast-ish enough to not let us run over by every car that passes by for being to slugish to react.
Such a stiuation, seeing to late an oncoming car that a healthy person would not have any problem with, was a very strong initiator of huge adrenaline spikes BTW when I was at my worst. Even if I was (barely) walking and the cars were still far away.
One could say: hey, but is creatine not meant to be that fast fuel? Well, I’d say it is *a* major fast fuel. But without those Na+/K+ co-transporters working good that might be not enough. We sure have them for some reason too.
When asking: would !!!MEDICALLY GUIDED!!! potassium supplementation solve all I’ll answer: “I wish” and “of coarse not”. But it has good potential to be a major overlooked part of the very complex puzzle.
Many of us might have genetic mutations in some of those (co-)transporters by the way, asking for a more thoughtful response / fix.
Same here as with POTS and MCAS: many thanks are due to Issie for fighting for so many years against the stream (and for keep on “nagging” me about impaired transporters) ;-).
Ha! You like me “nagging” you!
We sure have had an insightful, going on 2 years, time together. Learning a lot and uncovering science and making major connections.
Here’s to more discovery in our search for WHYs. Let’s discover some more “purple bandaids”.
I’m sure glad you, Dejurgen, have been in my life and that we can be partners in science and friendship.
You have an amazing brain and ability to connect the dots of very complex, complicated science. You amaze me! Truly, making your own place among those of truly great insight. Keep going, my friend. And continue to improve in health and find joy each day!
Issie
With “With that I mean: *increase* average “standy” energy / ATP production to be ready and available to use it any time when it is needed.” I meant increase “standBy” energy / ATP production.
I forgot to mention an important part of this “keep the engines running so we can react quick enough” idea:
Many cells can / may need to continously produce additional energy in order to have enough for when a quick increase in energy production and consumption is needed. When it’s not needed, the “excess” ATP / NADH /… will create excess (damaging) ROS.
Turning “excess” ATP / NADH /… production to heat as quickly as the “reserve bucket of it” is full is a good way to prevent them to rise to too dangerous levels creating deadly ROS storms. Still, even if “the bucket is full” you need to keep the engine iddling as very few ATP / NADH /… can be stored within the cells.
The amount of extra ATP / NADH /… the cells can store should only provide enough energy for just a (very) small instant of time. Anaerobic metabolism can’t pick up quickly enough. So on top of this very small amount of ATP / NADH /… you can safely stock in each cell you IMO need to keep producing extra energy *even* if that maximum (but tiny) storage is full. You just can’t turn mitochondria production up or down quick enough at all. And you need to keep wasting ATP / NADH /… to heat as long as you don’t need it in a burst of effort.
That is… …wastefull. Wouldn’t it be better to give that “excess” to other parts of the body that do a big effort AND can’t provide enough ATP for their needs even when their mitochondria run full steam?
If so, how could that be done? How could it get from places that don’t need it but produce it in excess, where it turns to heat waste at best and toxic levels of ROS at worst to places that badly crave and starve for it?
How about those cells that “need to keep their engines iddling and have to produce waste ATP”… dump it into the blood stream? With a bit of luck it’ll pass a bit later by a cell that needs it badly. If not, it can still be turned to heat or hopefully not excessive ROS elsewhere…
Isn’t that exactly the highly puzzling and unique thing Ron Davis discovered our ME cells do? Throw ATP out of their cells while we have a diseasse of massive energy shortage? Then maybe the “iddling engine + co-transporters imbalance” idea may help solve this enigma too?
And if the blood stream isn’t good enough to get it their fast enough, how about dumping ATP in the connective tissue fluids too? It’ll reach some extra cells needing the ATP I’d guess.
If things goes bad, dumping too much high energy chemicals like ATP into the connective tissue might cause some additional damage to it. Yet, that damage may still be worth the gains. We’d be more prone to EDS like symptoms (and FM!) for sure. But it could be better then our brain, heart, liver and nerve cells rapidely dying from lack of energy…
dejurgen
tho cannot process all u saying, still want u to know how immensely helpful is to ‘see’ a reason for this all which is so …….. explanatory.
cheers, sunie
Thanks for the appreciation sunny!
It’s complex indeed, both for making these things up, for trying to explain them somewhat understandably, and for understanding it.
Don’t worry, at worst I failed to read and understand more then ten lines of basic day to day texts.
For those who wish to read upon the ideas that Issie developped and shared over time related to this topic, I have some links to the dinet forum she shared her ideas on.
Keep in mind that she wrote all but one blog in 2010-2011. That may sound like outdated, but that is far from the truth. Some ideas might be less up to date, but many are as new today as they where then. She ran in front of much research results later going the direction of her ideas. I do find that always inspiring!
I didn’t participate in any of those conversations. I had the honor of being able to discuss those ideas with her personally. I also try and keep to a single forum to vent my thoughts. Cort provides a great one ;-). Thanks Cort for all what you have done for us over these years. Selecting, summarising and structuring isn’t always my strength so thanks for the much needed help here especially when I still had to “crawl back from the depths of ME hell”.
Here are the links. Enjoy and share if you appreciate them.
As six links wont pass WordPress’ spam filter, so add in front of all of them http://www.dinet.org/forums/topic/ or use a search engine searching for “dinet.org and the other info”.
15775-salt-and-hydration/
15806-some-out-of-the-box-thinking-need-some-feedback/
15830-more-on-aldosterone-and-renin/
15869-cortisol-aldosterone-hormone-support-would-it-help/
16668-renin-aldesterone-the-article/
27795-arterial-dysfunction-with-salt/
That should be sorted according to date of publication. Remember: leggacy doesn’t mean old nor junk, it means of remaining value ;-).
Thanks Dejurgen for posting for me. A bit of a ME day for me.
I hope some will get some helpful information from them.
I’m a bit of an “out of the box, flip the coin” thinker and have swam against the currant. If it didn’t make sense to me, I wanted to know WHY. I keep digging for those WHYs in search for the best “purple bandaids”?
Issie
http://www.dinet.org/forums/topic/15775-salt-and-hydration
http://www.dinet.org/forums/topic/15806-some-out-of-the-box-thinking-need-some-feedback/
http://www.dinet.org/forums/topic/15830-more-on-aldosterone-and-renin
http://www.dinet.org/forums/topic/15869-cortisol-aldosterone-hormone-support-would-it-help
http://www.dinet.org/forums/topic/16668-renin-aldesterone-the-article
http://www.dinet.org/forums/topic/27795-arterial-dysfunction-with-salt
I had trouble with getting one of the post to open as Dejurgen had to link them. Hope this works.
Cort –
Don’t know if you you may have seen this in the news. I don’t know anything about Dr. Joel Young but if he has some treatment that significantly improves life for CFS patients I would expect it to be public news? Have you read his book or heard anything specific on his treatment? It seems as though many doctors write books but none have an effective protocol that I am aware of for CFS. This does however drive desperate patients to their offices.
https://www.clickondetroit.com/health/2020/09/29/metro-detroit-woman-shares-her-battle-with-chronic-fatigue-syndrome/
How can we connect all those dots. We think, think and think. 🙂 Many intelligent people here. Also many intelligent scientist on our site. We still can’t see the light.
This disease is never going to be solved. The same with cancer. Science also has its limits.
Not all what I wrote in this moment of inspiration and deep exhaustion above double and triple checks out. The “keep the engines running hot” idea needs some major reworking. The main idea that a sizeable subgroup of ME (and / or subgroup of POTS) patients might have this “renin-aldosterone paradox” is still very much alive IMO.
from https://pubmed.ncbi.nlm.nih.gov/6428366/:
“Groups at Risk of Potassium Inadequacy
Potassium inadequacy can occur with intakes that are below the AI but above the amount required to prevent hypokalemia. The following groups are more likely than others to have poor potassium status.
People with inflammatory bowel diseases
Potassium is secreted within the colon, and this process is normally balanced by absorption [36]. However, in inflammatory bowel disease (including Crohn’s disease and ulcerative colitis), potassium secretion increases, which can lead to poor potassium status. Inflammatory bowel diseases are also characterized by chronic diarrhea, which can further increase potassium excretion [37].”
… (dejurgen note and a few other conditions).
The info given by Cort and me IMO still points to a too low potassium to sodium ratio being a good candidate to explain much of this “renin-aldosterone paradox”.
@Nancy B. and Maika: thanks for pointing to bradykinin!
from https://en.wikipedia.org/wiki/Bradykinin:
“Function
Effects
Bradykinin is a potent endothelium-dependent vasodilator and mild diuretic, which may cause a lowering of the blood pressure. It also causes contraction of non-vascular smooth muscle in the bronchus and gut, increases vascular permeability and is also involved in the mechanism of pain.[4]
During inflammation, it is released locally from mast cells and basophils during tissue damage.[5] Specifically in relation to pain, bradykinin has been shown to sensitize TRPV1 receptors, thus lowering the temperature threshold at which they activate, thus presumably contributing to allodynia.[6]”
As Cort wrote
” The low levels of Ang (1-7) found in this study suggested that ACE-2 enzyme activity was low.
Note that ACE-2 also cleaves or breaks up other peptides including bradykinin.”
Combined it says that (a large subgroup of) ME patients have increased bradikinin levels.
According to wikipedia:
“It also causes contraction of non-vascular smooth muscle in the bronchus and gut”
=> should make breathing more difficult (ME has well known “breathing abnormalities”)
=> could make gut movement (motility) worse => gut cramping and poor gut movement and hence chances for reduced digestion, bloating…
“increases vascular permeability”
=> eases transfer of fluids in and out the blood vessels. While that has its set of advantages, it also IMO makes blood pooling more easily happening (ME, POTS, ?MCAS?,…)
=> it also makes infiltration of immune cells from the blood towards the intercellular space (in between tissue and / or connective tissue) easier IMO increasing chances for easier inflammation, connective tissue issues (EDS…)
“involved in the mechanism of pain.” “bradykinin has been shown to sensitize TRPV1 receptors, thus lowering the temperature threshold at which they activate, thus presumably contributing to allodynia.”
=> increased pain sensitivity, pain “abnormalities” like tingling, neuropathic pain, burning sensations… seen in FM/ME/MCAS…
“During inflammation, it is released locally from mast cells and basophils during tissue damage.”
=> releasing a burst of bradykinin may IMO *well* be a (measured by its effects) a major contributor to some MCAS cases, next to histamin.
If so, patients with the combination low blood volumes, IBS and some form of orthostatic intolerance and / or MCAS (I had it for years (low level but for much of the day) without recognizing it, Issie helped me to better recognize it) may fit this “this renin-aldosterone paradox seems to talk about the ratio potassium to sodium and / or underlying mechanisms for it to go wrong.
This potential solution for the “renin-aldosterone paradox” may also help connecting a large cluster of disease ranging from ME / FM /POTS /MCAS / EDS … together in a novel way.
Special thanks this time for slicing, dicing and presenting all that info time and again in such a clear and readable way Cort!
“This potential solution for the “renin-aldosterone paradox” may also help connecting a large cluster of disease ranging from ME / FM /POTS /MCAS / EDS … together in a novel way.”
And IBS
I thought my narrowed blood vessels were a personal peculiarity. When I was in hospital last year they had to take blood from my ankle.
I just wanted to mention that after you wrote about phenylephrine in the last pots article, I found a prescription free flu medicament, containing phenylephrine and paracetamol = acetaminophen. Paracetamol, as a study says, enhances the effect of phenylephrine. Presumably vitamin c, which I take high dosageg, does the same. Long story short, I am much better by taking that flu medicament, doregrippin, with phenylephrine. I have for the first time since long no pain when I go to sleep, and it even saved me from my biggest fear last night, from gastroparesis, severe pain, collapse of the digestive system, unavoidable leading to a syncope, fainting. Whenever I take it not only the pain stops, I can for the first time feel the grip of the illness going away, the tension vanishes, the heart rhythm disturbances and inner restlessness is gone. Thank you.
Hi, I see those is an old thread but wanted to add my info. I now suffer from periodic paralysis episodes from low potassium (from long haul Covid), and my Aldosterone levels are off the charts. (Normal is like up to 25, my number was 99 and then tested again and was 129!)
I have the ME/CFS issues, but have just been focusing on the paralysis episodes as they are the most clearly debilitating. I take rx potassium and spirolactone. But still suffer from episodes.
I have me, pots, and MCAS – recent bloodwork found a high aldosterone to renin ratio but with low renin and normal aldosterone. Does this fit the picture of the POTS paradox? I’m feeling very confused at this point and not sure what the implications are. I have been taking two tsps a day of salt so does this mean I stop or continue that? Obviously will discuss with my specialists but also interested in what the hive mind thinks.
Has low blood volume been found in any other orthostatic intolerance syndromes apart from POTS?